Answer:
- 8 m from both : Constructive
- 11 m and 7 m : Constructive
- 10 m and 8 m : Destructive
- 11 m and 14 m : In between.
- 20 m and 12 m : Constructive
- 13 m and 19 m : Destructive
- 19 m and 14 m : In between.
Step-by-step explanation:
Equation of the wave
We know that the amplitude of a wave starting at
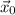 measured at position
measured at position
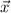 at time t is
at time t is
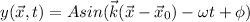
where
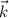 is the wavevector, ω the angular frequency, and φ the phase angle.
is the wavevector, ω the angular frequency, and φ the phase angle.
If we measure for a time
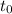 we get
we get
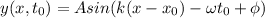
Now, we can use:
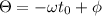
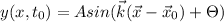
Finally, we can write this in term of the distance d, as
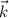 is parallel to the displacement vector for a sound wave:
is parallel to the displacement vector for a sound wave:
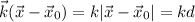
where k is the wavenumber
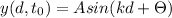
this is the amplitude of a sound wave measured at a distance d at time
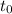
Interference
Measuring two identical waves at the same time, one starting at distance d and the other at distance d', the amplitude measured is:
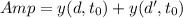
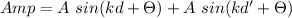
Constructive interference
We get constructive interference when both sines equals one, or minus one, so, we need a phase difference of
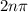 , where n is an integer :
, where n is an integer :
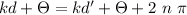
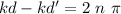
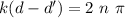
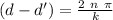
as the wavenumber is
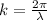
where
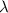 is the wavelength,
is the wavelength,
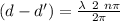
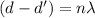
so, the difference between the distances must be a multiple of the wavelength to obtain constructive interference.
Destructive interference
We get destructive interference when one sin equals one, and the other minus one, so, we need a phase difference of
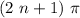 , where n is an integer
, where n is an integer
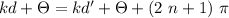
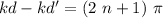
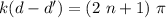
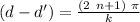
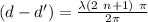
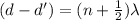
Problem
Knowing that
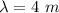
so, for the first
8 m from both :
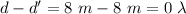
Constructive
11 m and 7 m:
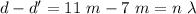
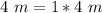
Constructive
10 m and 8 m
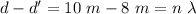
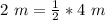
Destructive
11 m and 14 m
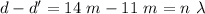
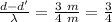
In between.
20 m and 12 m
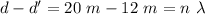
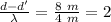
Constructive
13 m and 19 m
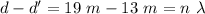
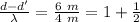
Destructive.
14 m and 19 m
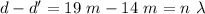
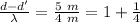
In between.