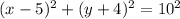Answer:
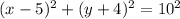
Explanation:
We need to find the equation of the circle. First, the formula:

Where (h,k) is the center and r is the radius
The center is (5,-4), so we can say:

Now, to find the radius, we can use the distance formula to find distance between (5,4) and (-3,2).
The distance formula is

Where
x_1 = 5
x_2 = -3
y_1 = 4
y_2 = 2
Plugging in, we get:
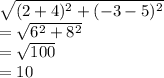
Hence, the radius is 10 and we can write the equation of circle as: