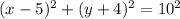Question

A circle is centered at the point (5,-4) and passes through the point (-3,2).

The equation of this circle is (x+ 1] 2+0+ 0
.
What is?

Answer 1

Answer:
`(x-5)^2+(y+4)^2=100`

Explanation:

Equation of circle having center at (h,k) :

`(x-h)^2+(y-k)^2=r^2`

Then, the equation of circle having center at (5,-4) and radius r will be:-

`(x-5)^2+(y-(-4))^2=r^2\\\\(x-5)^2+(y+4)^2=r^2` (1)

Since, circle is passes through (-3,2).

Put x= -3 and y=-2

`(-3-5)^2+(2+4)^2=r^2\\\\\Rightarrow\ 64+36=r^2\\\\\Rightarrow\ r^2=100`

Putting value of
`r^2=100` in (1), we get

`(x-5)^2+(y+4)^2=100`

Hence, the equation of this circle is
`(x-5)^2+(y+4)^2=100`

Answer 2

`(x-5)^2  + (y+4)^2 = 10^2`

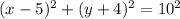
Explanation:

We need to find the equation of the circle. First, the formula:

`(x-h)^2 + (y-k)^2 = r^2`

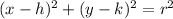
Where (h,k) is the center and r is the radius

The center is (5,-4), so we can say:

`(x-5)^2  + (y+4)^2 = r^2`

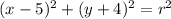
Now, to find the radius, we can use the distance formula to find distance between (5,4) and (-3,2).

The distance formula is
`√((y_2-y_1)^2 + (x_2-x_1)^2)`

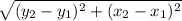
Where

x_1 = 5

x_2 = -3

y_1 = 4

y_2 = 2

Plugging in, we get:

`√((2+4)^2 + (-3-5)^2) \\=√(6^2 + 8^2)\\ =√(100) \\=10`

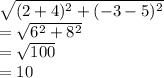
Hence, the radius is 10 and we can write the equation of circle as:

`(x-5)^2  + (y+4)^2 = 10^2`