Answer:
see explanation
Explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
Rearrange x - 2y = - 3 into this form
Subtract x from both sides
- 2y = - x - 3 ( divide all terms by - 2 )
y =
 x +
x +
 ← in slope- intercept form
← in slope- intercept form
with m =

• Parallel lines have equal slopes, thus
y =
 x + c ← is the partial equation
x + c ← is the partial equation
To find c substitute (- 1, 2) into the partial equation
2 = -
 + c ⇒ c = 2 +
+ c ⇒ c = 2 +
 =
=
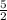
y =
 x +
x +
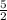 ← in slope- intercept form
← in slope- intercept form
Multiply through by 2
2y = x + 5 ( subtract 2y from both sides )
0 = x - 2y + 5 ( subtract 5 from both sides )
- 5 = x - 2y, thus
x - 2y = - 5 ← in standard form