Question

Find the distance between lines 8x−15y+5=0 and 16x−30y−12=0.

Answer 1

d =
`(11)/(17)`.

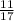Explanation:

We, have given two line lines 8x-15y+5=0 and 16x−30y−12=0. These two lines are parallel because it follows parallel condition:
`(a_1)/(a_2) = (b_1)/(b_2) \\eq  (c_1)/(c_2)`.

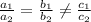We need to find the distance between these two parallel lines.

We know that distance formula, between two parallel line:

d =
`\frac c_1 - c_2 {\sqrt{A^(2) +B^(2)  } }`

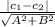
We have these two equation 8x−15y+5=0 and 16x−30y−12=0 but its coffiecients are not same, then we will first same coffiecients:

8x−15y+5=0, we can written as 8x-15y = -5

16x−30y−12=0, we can written as 16x-30y = 12, common 2 from these equation: 8x-15y = 12/2 = 6. Now, both lines have same cofficients.

Applying distance formula,

d =
`\frac -5 - (+6) {\sqrt{8^(2) +(-15)^(2)  } }`

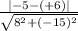
d =
`(|-11|)/(√(64 +225) )`

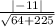
d =
`(|-11|)/(√(289) )`

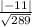
d =
`(11)/(17)`

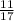
Therefore, distance between the these two lines are 11/17.

Answer 2

`(11)/(17)`

Explanation:

Lines
`8x-15y+5=0` and
`16x-30y-12=0` are parallel because

`(8)/(16)=(-15)/(-30)\\eq (5)/(-12)`

The distance between two lines
`a_1x+b_1y+c_1=0` and
`a_1x+b_1y+c_2=0` can be calculated using formula

`D=(|c_1-c_2|)/(√(a_1^2+b_1^2))`

Divide the equation of the second line by 2:

`8x-15y-6=0`

Hence, the distance between two lines is

`D=(|5-(-6)|)/(√(8^2+(-15)^2))=(|5+6|)/(√(64+225))=(11)/(√(289))=(11)/(17)`