Question

Find the area of the triangle defined by the coordinates (7,1). (0, 10), and (9,4). (To the nearest tenth)

Answer 1

19.5

Explanation:

The area of a triangle given 3 coordinates can be solved using the formula:

`Area=|(A_x(B_y-C_y)+B_x(C_y-A_y)+C_x(A_y-B_y))/(2)|`

Where

A_x is x coordinate of first point (here 7)

A_y is y coordinate of first point (here 1)

B_x is x coordinate of 2nd point (here 0)

B_y is y coordinate of 2nd point (here 10)

C_x is x coordinate of 3rd point (here 9)

C_y is y coordinate of 3rd point (here 4)

Plugging these into the formula, we get out answer:

`Area=|(A_x(B_y-C_y)+B_x(C_y-A_y)+C_x(A_y-B_y))/(2)|\\Area=|(7(10-4)+0(4-1)+9(1-10))/(2)|\\Area = |(7(6)+0+9(-9))/(2)|\\Area=|-19.5|\\Area = 19.5`

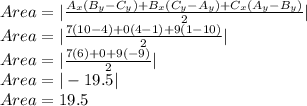
Hence, the area is 19.5