Answer:
y= -2x-5
Explanation:
First find the gradient of the first line
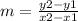
m=

m=
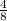
m=1/2
From this we can find the gradient of the perpendicular line, or the normal.
m1 × m2 = -1
Replace m1 with 1/2
1/2 × m2 = -1
m2= -2
Substitute values into
y-y1=m (x-x1)
y-3=-2 (x+4)
y-3=-2x -8
y=-2x-5