Question

SV perpendicular RT RSU=(17x-3) and UST=(6x-1) find each measure

Answer 1

Part 1) x=8

Part 2) m∠RSU=133°

Part 3) m∠UST=47°

Part 4) m∠WSV=43°

Part 5) m∠VSU=137°

Explanation:

see the attached figure to better understand the problem

Part 1) Find the value of x

we know that

m∠RSU and m∠UST are supplementary angles (by linear pair)

so

m∠RSU+m∠UST=180°

we have

m∠RSU=(17x-3)°

m∠UST=(6x-1)°

substitute the given values and solve for x

`(17x-3)\°+(6x-1)\°=180\°`

`(23x-4)=180`

`23x=180+4`

`23x=184`

`x=8`

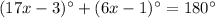
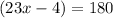
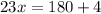
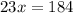
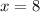
Part 2) Find the measure of m∠RSU

we have

m∠RSU=(17x-3)°

substitute the value of x

m∠RSU=17(8)-3=133°

Part 3) Find the measure of m∠UST

we have

m∠UST=(6x-1)°

substitute the value of x

m∠UST=6(8)-1=47°

Part 4) Find the measure of m∠WSV

we know that

m∠UST=m∠RSW -----> by vertical angles

so

m∠RSW=47°

m∠RSW+m∠WSV=90° ----> given problem (SV perpendicular RT)

substitute the value of m∠RSW and solve for m∠WSV

47°+m∠WSV=90°

m∠WSV=90°-47°=43°

Part 5) Find the measure of m∠VSU

we know that

m∠VSU=m∠VST+m∠UST

we have

m∠VST=90° ----> given problem (SV perpendicular RT)

m∠UST=47°

substitute

m∠VSU=90°+47°=137°