Answer:
The rate of interest was approx 5.64%.
Explanation:
The compound interest formula is :

Here p = 4400
r = ?
n = 1
t = 5
A = 5790
Now putting the values in formula we get;
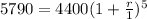
=>
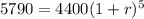
=>
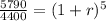
=>
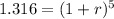
=>
![1+r=\sqrt[5]{1.316}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ra50h4cb8dcyk8kj0dehoz9t2b2w814zr1.png)
r = 0.0564
In percentage it is
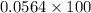 = 5.64%
= 5.64%
Hence, the rate of interest was approx 5.64%.