Question

Viola and Paige stand next to each other and kick soccer balls in the air. The

path of Viola's ball is described by the equation y=-3x2 + 6x + 3. The path of
Paige's ball is shown by the graph.
In each function, x is the horizontal distance the ball travels in meters, and y
represents the height.
Whose soccer ball reaches a greater height?
O
A. Both soccer balls reach the same height
O
B. Viola's soccer ball
O
C. Paige's soccer ball

Answer 1

C. Paige's soccer ball.

Explanation:

When you graph y = 3x^2 + 6x + 3, you can see that the max of the parabola is around 6. This is lower compared to Paige's soccer ball's max height shown in the image.

Answer 2

C. Paige's soccer ball

Explanation:

To solve this problem, we just need to graph Viola's function to know the altitude she reached, and then compare it with Paige's altitude.

So, we know that Viola's function is
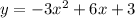`y=-3x^(2)+6x+3`, as an extra solution, we can calculate the vertex of this quadratic function, that will give us Viola's max altitude.

`V(v_(x);v_(y))\\V((-b)/(2a);f(v_(x) ))`

Where b and a are from the general quadratic function:
`y=ax^(2) +bx+c`.

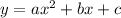So, in this case, a = -3; b = 6. Replacing this values, we find the vertex:

`V((-b)/(2a);f(v_(x) ))`

`v_(x)= (-b)/(2a)=(-6)/(2(-3))=1`

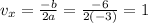
Then, we use the function to calculate the vertical coordinate of the vertex:

`v_(y)=f(1)=-3(1)^(2)+6(1)+3=-3+6+3=6`

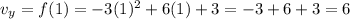
Therefore, the max altitude reached by Viola is 6 meters.

Now, from the graph, we observe that Paige's max altitude is around 7.5 meters.

Therefore, Paige reached the higher height. The answer is C.