Simplification of
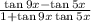 is tan 4x
is tan 4x
Solution:
By using sum-difference formula for tangent,
Tangent of difference between two angles is written as,
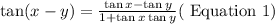
By comparing the above equation 1 with
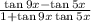 ,
,
we get x = 9x and y = 5x
By substituting x = 9x and y = 5x in equation 1,
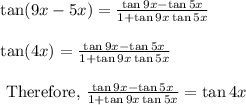
Hence by using difference formula for tangent,
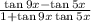 is simplified as tan4x
is simplified as tan4x