Question

A movie theater advertises that a family of two adults, one student, and one child between the ages of 3 and 8 can attend a movie for $15. An adult ticket costs as much as the combined cost of a student ticket and a child ticket. you purchase 1 adult ticket, 4 student tickets, and 2 child tickets for $23.

what are 3 system of equations?

what is the price per ticket for each type of ticket?

Answer 1

The price per ticket for adults is $5

The price per ticket for students is $4

The price per ticket for child between the ages of 3 and 8 is $1

Explanation:

Let

x -----> the price per ticket for adults

y -----> the price per ticket for students

z -----> the price per ticket for child between the ages of 3 and 8

we know that

The system of equations is

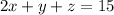`2x+y+z=15` ------> equation A

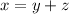`x=y+z` ------> equation B

`x+4y+2z=23` -----> equation C

substitute equation B in equation A and solve for x

`2x+(x)=15`

`3x=15`

`x=5`

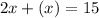
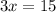
Substitute the value of x in equation B and equation C

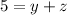`5=y+z` -----> equation B

`5+4y+2z=23`

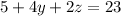
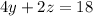`4y+2z=18` -----> equation C

Solve the system by graphing

Remember that the solution is the intersection point both graphs

Using a graphing tool

The solution is the point (1,4)

so

z=1, y=4

therefore

The price per ticket for adults is $5

The price per ticket for students is $4

The price per ticket for child between the ages of 3 and 8 is $1