Question

Using the graph as your guide, complete the following statement.

The discriminant of the function is

Answer 1

Answer: The answer is A because the vertex lies on the x axis which makes it zero.

Answer= A

Answer 2

Using the graph as your guide, complete the following statement.

The discriminant of the function is

Step-by-step explanation: Remember a parable of the form f(x) = a
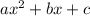`a x^(2) + bx + c`, satisfy:

(1) has only one root if and only if [tex] b^2 - 4ac = 0[\tex]

(2) has two real roots if and only if [tex] b^2 - 4ac > 0[\tex]

(3) has two complex roots if and only if [tex] b^2 - 4ac < 0[\tex].

The number b^2 - 4ac is called the discriminant of the parable f(x).

From the graph we can see that the parable has only one root approx in x =1. Thus from point (1) we can conclude that the discriminant should be zero.

PD: a root of a polynomial f(x) is a number a such thast f(a) =0.

The answer is A.