Question

Find the length of side AB.

Give your answer to 3 significant figures.
C
410
13.5 cm
A
B

ANSWER:
sin41 × 13.5 = 8.85679
rounded to 3 sig fig
= 8.57​

Answer 1

8.86 cm

Explanation:

The sine rule shows the relationship between the sides of a triangle and its opposite sides. Sine rule states that given a triangle with side a and opposite angle A, side b and opposite angle B, side c and opposite angle C then:

`(a)/(sin(A)) =(b)/(sin(B))=(c)/(sin(C))`

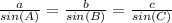
From the image attached, let AB = x, its opposite angle is 41°. BC = 13.5 cm and its opposite angle is 90° (right angle). Therefore using sine rule:

`(x)/(sin(41)) =(13.5)/(sin(90)) \\\\x=sin(41)*(13.5)/(sin(90))\\\\x=8.8568\\\\ x=8.86\ cm\ to\ 3\ s.f`

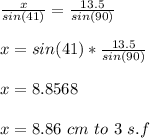
x = AB = 8.86 cm