Question

In a compression test, a steel test specimen (modulus of elasticity = 30 x 106lb/in2) has a starting height= 2.0 in and diameter = 1.5 in. The metal yields (0.2% offset) at a load = 140,000 lb. At a load of 260,000 lb, the height has been reduced to 1.6 in. Determine (a)yield strength and (b) flow curve parameters (strength coefficient and strain-hardening exponent). Assume that the cross-sectional area increases uniformly during the test.

Answer 1

Step-by-step explanation:

A) we know that volume is given as V

`V  =(\pi)/(4) D^2 h`

where D = 1.5 in , h = 2.0 in

so
`V = (\pi)/(4) 1.5^2* 2 = 3.53in^3`

`Area =(\pi)/(4) D^2 = (\pi)/(4) * 1.5^2 = 1.76 in^4`

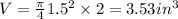
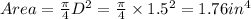
yield strenth is given as
`\sigma_y = (force)/(area) = (140,000)/(1.76)`

`\sigma_y = 79.224 ksi`

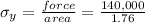
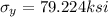
b)

elastic strain
`\epsilon = (\sima_y)/(E) = (79.224)/(30* 10^3) = 0.00264`

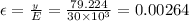
strain offsets = 0.00264 + 0.002 = 0.00464 [where 0.002 is offset given]

`(\delta)/(h) = 0.00464`

`(h_i -h_o)/(h_o) = 0.00464`

`h_i = 2*(1-0.00464) = 1.99 inch`

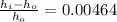
area
`A = (volume)/(height) = (3.534)/(1.9907) = 1.775 in^2`

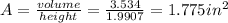
True strain
`\sigma = (force)/(area) = (140,000)/(1.775 in^2) = 78,862 psi`

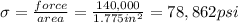
At P= 260,000 lb ,
`A = (3.534)/(1.6) = 2.209 inc^2`

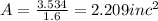
true stress
`\sigma  = (260,000)/(2.209) = 117,714 psi`

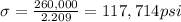
true strain
`\epsilon = ln(2)/(1.6) = 0.223`

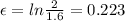
flow curve is given as \sigma = k\epsilon^n

`\sigma_1 = 78,862 psi`

`\epsilon_1 = 0.00464`

`\sigma_2 = 117,714 psi`

`\epsilon_2 = 0.223`

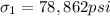
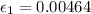
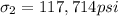
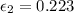
so flow curve is

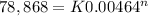`78,868 = K 0.00464^n` .........1

`117,714 = K 0.223^n` .........2

Solving 1 and 2

we get

n = 0.103

and K =137,389 psi

Strength coffecient = K = 137.389ksi

strain hardening exponent = n = 0.103