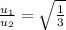Question

2. Two projectiles thrown from the same point at angles 0,=60° and 02=30° with the horizontal,

attain the same height. What is the ratio of their initial velocities (Voi:Voz)?
​

Answer 1

The answer is below

Step-by-step explanation:

The maximum height (h) of a projectile with an initial velocity of u, acceleration due to gravity g and at an angle θ with the horizontal is given as:

`h=(u^2sin^2\theta)/(2g)`

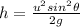
Given that the two projectile has the same height.

`For\ the\ first\ projectile\ with\ an\ angle\ \60^0 \ with\ the\ horizontal\ and initial\ velocity\ u_1:\\\\h=(u_1^2sin^260)/(2g) =(0.75u_1^2)/(2g) \\\\For\ the\ second\ projectile\ with\ an\ angle\ \30 \ with\ the\ horizontal\ and initial\ velocity\ u_2:\\\\h=(u_2^2sin^230)/(2g) =(0.25u_2^2)/(2g)\\\\(0.25u_2^2)/(2g)=(0.75u_1^2)/(2g)\\\\0.25u_2^2=0.75u_1^2\\\\(u_1^2)/(u_2^2) =(0.25)/(0.75) \\\\(u_1^2)/(u_2^2)=(1)/(3) \\`
`\\(u_1)/(u_2)=\sqrt(1)/(3)`