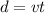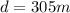Answer:
Part a)
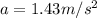
Part b)
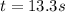
Part c)
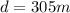
Step-by-step explanation:
Part a)
Car start from rest and reached to final speed of 19 m/s when it will cover a distance of 126 m
So we will have
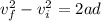
now we will have
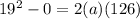
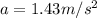
Part b)
in order to find the time taken by the car we can use another kinematics equation
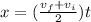
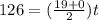
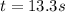
Part c)
If the traffic on free way is moving with speed 23 m/s
so we can say that traffic will move by distance