Question

Erase all the trajectories, and fire the pumpkin vertically again with an initial speed of 14 m/s. As you found earlier, the maximum height is 9.99 m. If the pumpkin isn't fired vertically, but at an angle less than 90∘, it can reach the same maximum height if its initial speed is faster. Set the initial speed to 22 m/s, and find the angle such that the maximum height is roughly the same. Experiment by firing the pumpkin with many different angles. What is this angle?

Answer 1

`\theta=39.49^(\circ)`

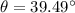
Step-by-step explanation:

Maximum height of the pumpkin,
`H_(max)=9.99\ m`

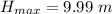
Initial speed, v = 22 m/s

We need to find the angle with which the pumpkin is fired. the maximum height of the projectile is given by :

`H_(max)=(v^2\ sin^2\theta)/(2g)`

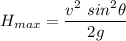
On rearranging the above equation, to find the angle as :

`\theta=sin^(-1)(\frac{\sqrt{2gH_(max)}}{v})`

`\theta=sin^(-1)((√(2* 9.8* 9.99))/(22))`

`\theta=39.49^(\circ)`

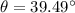
So, the angle with which the pumpkin is fired is 39.49 degrees. Hence, this is the required solution.