Question

A certain stock exchange designates each stock with a one-, two-, or three-letter code, where each letter is selected from the 26 letters of the alphabet. If the letters may be repeated and if the same letters used in a different order constitute a different code, how many different stocks is it possible to uniquely designate with these codes? a. 2,951 b. 8,125 c. 15,600 d. 16,302 e. 18,278

Answer 1

e.18278

Explanation:

We are given that a certain stock exchanges designates each stock with a one, two or three letter code, where each letter is selected from the 26 letters of the alphabet.

Total number of letters=26

If code is made from one letter

Then , total number of ways=26

If code is made from two letters and repetition is allowed

Then , total number of ways=
`26* 26=676`

If code is made form three letter and repetition is allowed

Then, total number of ways=
`26* 26* 26=17576`

Total number of ways=26+676+17576=18278 ways

Hence, number of different stocks designated with these codes=18278.

Answer:e.18278

Answer 2

Answer: Option 'e' is correct.

Explanation:

Since we have given that

Number of letters of the alphabet = 26

Number of letters in code :

One letter code, or two letter code, or three - letter code.

Since repetition of letters are allowed, then

if it is one letter code, the number of arrangement would be 26.

If it is two letter code, the number of arrangements would be

`26* 26\\\\=26^2\\\\=676`

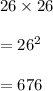
If it is three letter code, the number of arrangements would be

`26* 26* 26\\\\=26^3\\\\=17576`

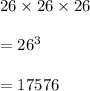
So, Number of different stocks to uniquely designate with these codes would be

`26+676+17576\\\\=18278`

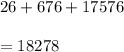
Hence, Option 'e' is correct.