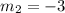Answer:
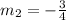 -- (a)
-- (a)
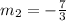 -- (b)
-- (b)
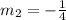 --- (c)
--- (c)
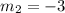 -- (d)
-- (d)
Explanation:
Given
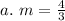
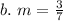
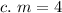

Required
Determine the slope of a perpendicular line
In geometry, the condition for perpendicularity is:

This formula will be applied in solving these questions.
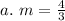

Substitute 4/3 for m
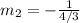
Express as a proper division
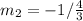
Convert to *

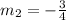
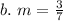

Substitute 3/7 for m
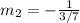
Express as a proper division

Convert to *
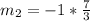
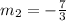
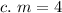

Substitute 4 for m
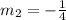


Substitute 1/3 for m
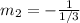
Express as a proper division
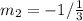
Convert to *