Question

Which step is part of a proof showing the opposite sides of parallelogram ABCD are congruent?

A) show that AC is congruent to BD
B) show that AD is congruent to AB Reactivate
C) show that angles A and D are supplementary
D) show that triangle ADB is congruent to triangle CB

Answer 1

its d

Explanation:

Answer 2

:D Show that triangle ADB is congruent to triangle CBD

Explanation:

We are given that a parallelogram ABCD .

We have to find which step is part of a proof showing the opposite sides of parallelogram ABCD are congruent.

We have to prove that opposite sides of parallelogram ABCD are congruent.

Given:ABCD is a parallelogram

AB is parallel to CD and BC is parallel to AD.

AB=CD and AD=BC

Construction:Join B and D.

Proof:In triangle ADB and triangle CBD

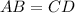`AB=CD` (given )

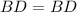`BD=BD` (reflexive property)

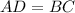`AD=BC` (given)

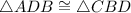`\triangle ADB\cong \triangle CBD` (SSS postulates)

`AD\cong BC` and
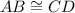`AB\cong CD` (CPCT)

Hence, option D is true.

Answer:D Show that triangle ADB is congruent to triangle CBD