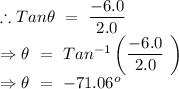Answer:
Part (a) a + b = (8.0i - 2.0j) and
 from the x-axis
from the x-axis
Part (b) b - a = (2.0i - 6.0j) and
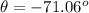 from the x- axis
from the x- axis
Step-by-step explanation:
Given,
From the addition of the two vectors,
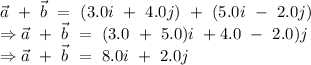
Let
 be the angle of the resultant vector of the addition of the vectors with the x-axis (i).
be the angle of the resultant vector of the addition of the vectors with the x-axis (i).
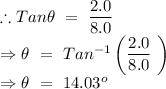
Part (b)
From the subtraction of the two vectors,

Let
 be the angle of the resultant vector of the addition of the vectors with the x-axis (i).
be the angle of the resultant vector of the addition of the vectors with the x-axis (i).