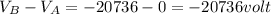Question

A particle with a charge of -4.0 μC and a mass of 3.2 x 10-6 kg is released from rest at point A and accelerates toward point B, arriving there with a speed of 72 m/s. The only force acting on the particle is the electric force. What is the potential difference VB - VA between A and B? If VB is greater than VA, then give the answer as a positive number. If VB is less than VA, then give the answer as a negative number.

Answer 1

`V_B-V_A=-20736-0=-20736volt`

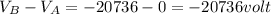
Step-by-step explanation:

We have given charge on the particle
`q=-4\mu C=-4* 10^(-6)C`

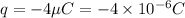
Mass of the charge particle
`m=3.2* 10^(-6)kg`

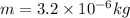
From energy of conservation kinetic energy will be equal to potential energy

So at point A

`(1)/(2)mv^2=qV`

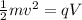
At point a velocity is zero

So
`(1)/(2)(3.2*10^(-6) )0^2=-4* 10^(-6)V_a`

`V_A=0volt`

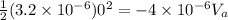
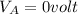
At point B velocity will be 72 m/sec

So
`(1)/(2)* 3.2* 10^(-6)72^2=-4* 10^(-6)V_b`

`V_B=-20736volt`

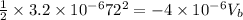
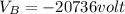
So
`V_B-V_A=-20736-0=-20736volt`