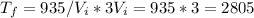Question

A rigid tank whose volume is unknown is divided into two parts by a partition. One side of the tank contains an ideal gas at 935°C. The other side is evacuated and has a volume twice the size of the part containing the gas. The partition is now removed and the gas expands to fill the entire tank. Heat is now transferred to the gas until the pressure equals the initial pressure. Determine the final temperature of the gas.

Answer 1

2805 °C

Step-by-step explanation:

If the gas in the tank behaves as ideal gas at the start and end of the process. We can use the following equation:

`P=RTn/V`

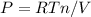
The key issue is identify the quantities (P,T, V, n) in the initial and final state, particularly the quantities that change.

In the initial situation the gas have an initial volume
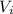`V_(i)`, temperature
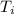`T_(i)`, and pressure
`P`,.

And in the final situation the gas have different volume
`V_(f)` and temeperature
`T_(f)`, the same pressure
`P`,, and the same number of moles
`n`,.

We can write the gas ideal equation for each state:

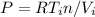`P=RT_(i)n/V_(i)` and
`P=RT_(f)n/V_(f)`, as the pressure are equals in both states we can write

`RT_(i)n/V_(i) = RT_(f)n/V_(f)`

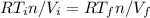
solving for
`T_(f)`

`T_(f) = T_(i)/V_(i) * V_(f)` (*)

We know
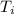`T_(i)` = 935 °C, and that the
`V_(f)` (the complete volume of the tank) is the initial volume
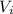`V_(i)` plus the part initially without gas which has a volume twice the size of the initial volume (read in the statement: the other side has a volume twice the size of the part containing the gas). So the final volume
`V_(f)= V_(i) + 2V_(i)=3V_(i)`

Replacing in (*)

`T_(f) = 935/V_(i) * 3V_(i) = 935*3= 2805`