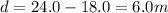Answer:
6.0 m below the top of the cliff
Step-by-step explanation:
We can find the velocity at which the ball dropped from the cliff reaches the ground by using the SUVAT equation
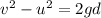
where
u = 0 (it starts from rest)
g = 9.8 m/s^2 (acceleration of gravity, we assume downward as positive direction)
h = 24 m is the distance covered
Solving for h,
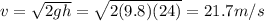
So the ball thrown upward is launched with this initial velocity:
u = 21.7 m/s
From now on, we take instead upward as positive direction.
The vertical position of the ball dropped from the cliff at time t is
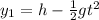
While the vertical position of the ball thrown upward is
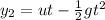
The two balls meet when
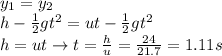
So the two balls meet after 1.11 s, when the position of the ball dropped from the cliff is

So the distance below the top of the cliff is