Answer:
1083.173 km
Step-by-step explanation:
Speed of longitudinal waves = 9.1 km/s
Speed of transverse waves = 5.7 km/s
Time taken by the longitudinal wave is t
Time taken by the transverse wave is t+71
Distance = Speed × Time
Distance traveled by the longitudinal wave
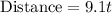
Distance traveled by the transverse wave
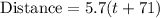
Since both distances are equal
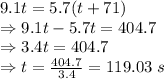
The time taken by the longitudinal wave is 119.03 seconds
Distance traveled by the longitudinal wave
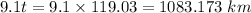
The earthquake is 1083.173 km away