Answer: 0.504772
Explanation:
Given : The sugar content of the syrup is canned peaches is normally distributed. Assume the can is designed to have standard deviation
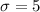 milligrams.
milligrams.
A random sample of n = 10 cans is studied.
Then, the sampling distribution of the sample variance is chi-square (
 ) distribution witth
) distribution witth
 degrees of freedom.
degrees of freedom.
Sample standard deviation:
 milligrams.
milligrams.
Test statistic for chi-square =
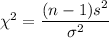
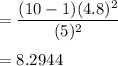
By using the chi-square distribution table , the chance of observing the sample standard deviation greater than 4.8 milligrams will be :-
P-value =
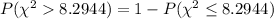
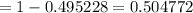
Hence, the chance of observing the sample standard deviation greater than 4.8 milligrams = 0.504772