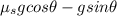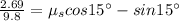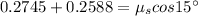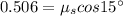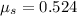Question

An untethered block sits on a flatbed truck as it accelerates up an incline that makes an angle of 15° with respect to the horizontal. If the truck speeds up at a rate less than 2.69 m/s2, the block remains on the truck. If the truck speeds up at a rate equal to or greater than this value, however, the block slides off the truck. What is the coefficient of static friction between the truck and the block?

Answer 1

The coefficient of static friction is 0.524

Solution:

As per the question:

Angle made with the horizontal,
`\theta = 15^(\circ)`

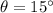
Acceleration of the truck, a = 2.69
`m/s^(2)`

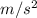
Now,

Forces are balanced along the x- direction:

When the block sits at rest and is about to slide:

`F_(s) - mgsin\theta = 0` (1)

Also, static force of friction,
`F_(s)`:

`F_(s) = \mu_(s)N`

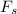where

N = mgcos
`\theta`

Thus

`F_(s) = \mu_(s)mgcos\theta` (2)

Now, from eqn (1) and eqn (2):

`\mu_(s)mgcos\theta - mgsin\theta = 0`

`\mu_(s) = tan\theta`

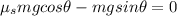
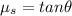
Also,

a =
`\mu_(s)gcos\theta - gsin\theta`

`(2.69)/(9.8) = \mu_(s)cos15^(\circ) - sin15^(\circ)`

`0.2745 + 0.2588 = \mu_(s)cos15^(\circ)`

`0.506 = \mu_(s)cos15^(\circ)`

`\mu_(s) = 0.524`