Answer:
The maximum number of pounds of potato salad that Charlie can buy is 0.375
Explanation:
see the attached figure to better understand the problem
Let
a ----> the cost of one tuna sandwich
b ----> the cost of a bottle of apple juice
c ----> the cost per pound of potato salad
x ----> pounds of potato salad
we have
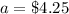
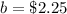
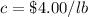
we know that
He wants to buy a tuna sandwich, a bottle of apple juice, and x pounds of potato salad and can spend up to $8
The inequality that represent this situation is
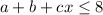
substitute the given values
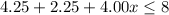
Solve for x
Combine like terms
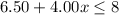
Subtract 6.50 both sides
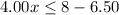

Divide by 4 both sides
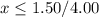

therefore
The maximum number of pounds of potato salad that Charlie can buy is 0.375