Question

I have 10 goats, n of which are male. I need to choose 2 of them to make a casserole.

The probability both of my choices are male is 2/15


Use the information to form an appropriate quadratic equation N square + an + b = 0, specifying the constants a and b.

Answer 1

Answer: There are 4 male goats.

Explanation:

We know that n of the 10 goats are male.

The probability that in a random selection, the selected goat is a male, is equal to the quotient between the number of male goats (n) and the total number of goats (10)

The probability is;

p = n/10

Now the total number of goats is 9, and the number of male goats is n -1

then the probability of selecting a male goat again is:

q = (n-1)/9

The joint probability (the probability that the two selected goats are male) is equal to the product of the individual probabilities, this is

P = p*q = (n/10)*((n-1)/9)

And we know that this probability is equal to 2/15

Then we have:

(n/10)*((n-1)/9) = 2/15

(n*(n-1))/90 = 2/15

n*(n-1) = 90*2/15 = 12

n^2 - n = 12

n^2 - n - 12 = 0

This is a quadratic equation, we can find the solutions if we use Bhaskara's formula:

For an equation:

a*x^2 + b*x + c = 0

The two solutions are given by:

`x = (-b +- √(b^2 - 4*a*c) )/(2*a)`

For our case, the solutions will be:

`n = (1 +- √((-1)^2 - 4*1*(-12)) )/(2*1 ) = (1+- 7)/(2)`

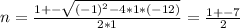
The two solutions are:

n = (1 - 7)/2 = -3 (this solution does not make sense, we can not have a negative number of goats)

The other solution is:

n = (1 + 7)/2 = 4

This solution does make sense, this means that we have 4 male goats.