Question

Viktor deposits $4,300 in an account that

carns 6% interest compounded monthly.
How much is in the account after five years?

Answer 1

Viktor will have $5,800 in his account after 5 years

Explanation:

Compound Interest

It happens when interest in the next period is then earned on the principal sum plus previously accumulated interest.

The formula is:

`\displaystyle A=P\left(1+{\frac {r}{n}}\right)^(nt)`

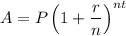
Where:

A = final amount

P = initial principal balance

r = interest rate

n = number of times interest applied per time period

t = number of time periods elapsed

Viktor deposits P=$4,300 in an account that earns r=6% interest compounded monthly. Since there are 12 months in a year, n=12. The interest rate is converted to decimal: r=6/100=0.06. The final amount in the account after t=5 years is:

`\displaystyle A=\$4,300\left(1+{\frac {0.06}{12}}\right)^(12*5)`

`\displaystyle A=\$4,300\left(1.005}\right)^(60)`

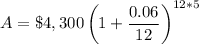
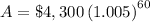
Calculating:

A = $5,800

Viktor will have $5,800 in his account after 5 years