Question

A boat travels at 15 m/s in a direction 45° east of north. The boat then turns and travels at 18 m/s in a direction 5°

north of east.
What is the magnitude of the boat's resultant velocity? Round your answer to the nearest whole number.
m/s
What is the direction of the boat's resultant velocity? Round your answer to the nearest whole degree.
º north of east

Answer 1

The magnitude of the boat's resultant velocity is 31.0 m/s

The direction of the boat's resultant velocity is 23.0° north of east

Step-by-step explanation:

A boat travels at 15 m/s in a direction 45° east of north

The vector of velocity is 15 m/s in direction 45° with north

The horizontal component = 15(m/s) sin(45)° = 10.61 m/s

The vertical component = 15(m/s) cos(45)° = 10.61 m/s

The boat then turns and travels at 18 m/s in a direction 5° north of east

The vector of velocity is 18 m/s in direction 5° with east

The horizontal component = 18(m/s) cos(5)° = 17.93 m/s

The vertical component = 18(m/s) sin(5)° = 1.57 m/s

The horizontal component of the resultant velocity x is

x = 10.61 + 17.93 = 28.54 m/s

The vertical component of the resultant velocity y is

y = 10.61 + 1.57 = 12.18 m/s

The magnitude of the resultant velocity
`R=\sqrt{x^(2)+y^(2)}`

`R=\sqrt{(28.54)^(2)+(12.18)^(2)}=31.03`

R ≅ 31.0 m/s

The direction of the resultant velocity is
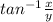`tan^(-1)(x)/(y)` north of east

The direction of the resultant velocity is
`tan^(-1)(12.18)/(28.54)=23.1`

α = 23.0° north of east

The magnitude of the boat's resultant velocity is 31.0 m/s

The direction of the boat's resultant velocity is 23.0° north of east