Question

A car is able to stop with an acceleration of − 3.00 m/s^2. Justify the mathematical routine used to calculate the distance required to stop from a velocity of 100.0 km/h by choosing the correct answer below.

A.) 16.7m because the average velocity is 50 km/h, the change in velocity divided by the acceleration is the time, and the time multiplied by the average velocity is the distance.
B.) 64.4m because the average velocity is 13.9 m/s, the average velocity divided by the acceleration is the time, and the time multiplied by the average velocity is the distance.
C.) 129m because the average velocity is 13.9 m/s, the change in velocity divided by the acceleration is the time, and the time multiplied by the average velocity is the distance.
D.) 257m because the initial velocity is 27.8 m/s, the initial velocity divided by the acceleration is the time, and the time multiplied by the initial velocity is the distance.

Answer 1

129 m because the average velocity is 13.9 m/s, the change in velocity

divided by the acceleration is the time, and the time multiplied by the

average velocity is the distance. ⇒ answer C

Step-by-step explanation:

Lets explain how to solve the problem

The given is:

The care is able to stop with an acceleration of -3 m/s²

→ The final velocity = 0 and acceleration = -3 m/s²

Calculate the distance required to stop from a velocity of 100 km/h

→ Initial velocity = 100 km/h

At first we must to change the unite of the initial velocity from km/h

to m/s because the units of the acceleration is m/s²

→ 1 km = 1000 meters and 1 hr = 3600 seconds

→ 100 km/h = (100 × 1000) ÷ 3600 = 27.78 m/s

The initial velocity is 27.78 m/s

Acceleration is the rate of change of velocity during the time,

then the time is the change of velocity divided by the acceleration

→
`t=(v-u)/(a)`

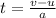
where v is the final velocity, u is the initial velocity, t is the time and

a is the acceleration

→ v = 0 , u = 27.78 m/s , a = -3 m/s²

Substitute these values in the rule

→
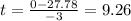`t=(0-27.78)/(-3)=9.26` seconds

The time to required stop is 9.26 seconds

We can calculate the distance by using the rule:

→ s = ut +
`(1)/(2)` at²

→ u = 27.78 m/s , t = 9.26 s , a = -3 m/s²

Substitute these values in the rule

→ s = 27.78(9.26) +
`(1)/(2)` (-3)(9.26) = 128.6 ≅ 129 m

The distance required to stop is 129 m

Average velocity is total distance divided by total time

→ Total distance = 129 m and total time = 9.26 s

→ average velocity = 129 ÷ 9.26 = 13.9 m/s

The average velocity is 13.9 m/s

So the time multiplied by the average velocity is the distance

The answer is C

129 m because the average velocity is 13.9 m/s, the change in

velocity divided by the acceleration is the time, and the time

by the average velocity is the distance.