Answer:
Part a)
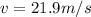
Part b)
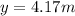
So he will not able to block the goal
Part c)

yes he can stop the goal
Step-by-step explanation:
As we know by the equation of trajectory of the ball

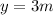
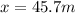
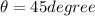
now from above equation we have
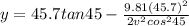
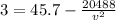
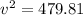
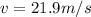
Part b)
If lineman is 4.6 m from the football


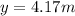
So he will not able to block the goal
Part c)
If lineman is 1 m from the football

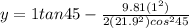

yes he can stop the goal