Question

A mail carrier parks her postal truck and delivers packages. To do so, she walks east at a speed of 0.80 m/s for 4.0 min, then north at a speed of 0.50 m/s for 5.5 min, and finally west at a speed of 1.1 m/s for 2.8 min. Define east as +x and north as +y. (a) Write unit-vector velocities for each of the legs of her journey. (b) Find unit-vector displacements for each of the legs of her journey. (c) Find her net displacement from the postal truck after her journey is complete.

Answer 1

Step-by-step explanation:

Given that,

She walks in east,

Speed = 0.80 m/s

Time = 4.0 min

In north,

Speed = 0.50 m/s

Time = 5.5 min

In west,

Speed = 1.1 m/s

Time = 2.8 min

(a). We need to calculate the unit-vector velocities for each of the legs of her journey.

The velocity of her in east

`\vec{v_(1)}=0.80\ \hat{x}\ m/s`

`\vec{v_(2)}=0.50\ \hat{y}\ m/s`

`\vec{v_(3)}=1.1\ \hat{-x}\ m/s`

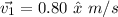
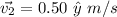
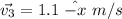
(b). We need to calculate the unit-vector displacements for each of the legs of her journey

Using formula of displacement

`\vec{d_(1)}=v_(1)* t_(1)`

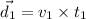
In east ,

`\vec{d_(1)}=0.80*4.0*60`

`\vec{d_(1)}=192\ \hat{x}\ m`

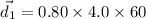
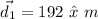
In north,

`\vec{d_(2)}=0.50*5.5*60`

`\vec{d_(2)}=165\ \hat{y}\ m`

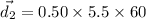
In west,

`\vec{d_(3)}=1.1*2.8*60`

`\vec{d_(3)}=184.8\ \hat{-x}\ m`

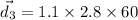
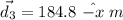
(c). We need to calculate the net displacement from the postal truck after her journey is complete

`\vec{d}=\vec{d_(1)}+\vec{d_(2)}+\vec{d_(3)}`

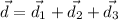
Put the value in the formula

`\vec{d}=192\hat{x}+165\hat{y}+184.8\hat{-x}`

`\vec{d}=7.2\hat{x}+165\hat{y}`

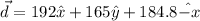
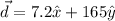
We need to calculate the magnitude of the displacement

`d=√((7.2)^2+(165)^2)`

`d=165.16\ m`

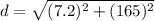
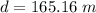
The magnitude of the displacement is 165.16 m.

Hence, This is the required solution.