Let
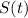 be the amount of sugar in the tank at time
be the amount of sugar in the tank at time
 .
.
a. The tank contains only pure water at the start, so
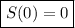 .
.
b. The inflow rate of sugar is
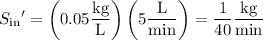
and the outflow rate is
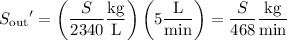
so the net rate at which
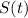 changes over time is governed by
changes over time is governed by

Multiply both sides by
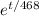 ,
,

and condense the left side as the derivative of a product,
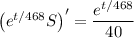
Integrate both sides to get

and solve for
 :
:
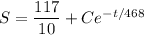
With
 , we find
, we find
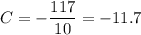 , so that
, so that
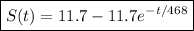
c. As
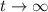 , the exponential term will converge to 0, leaving a fixed amount of 11.7 kg of sugar in the solution.
, the exponential term will converge to 0, leaving a fixed amount of 11.7 kg of sugar in the solution.