Question

Suppose babies born after a gestation period of 32 to 35 weeks have a mean weight of 2700 grams and a standard deviation of 800 grams while babies born after a gestations period of 40 weeks have a mean weight of 2900 grams and a standard deviation of 385 grams. If a 32-week gestation period baby weighs 2450 grams and a 41 week gestation period baby weights 2650 grams, find the corresponding z-scores. Which baby weighs less relative to the gestations period? The 32 week gestations period weighs _______ standard deviations above or below the mean. The 41 week gestations period weighs _______ standard deviations above or below the mean. (Round to two decimals places as needed) Which baby weighs relatively less? a. The baby born in week 41 does since its z-score is larger. b. The baby born in week 32 does since its z-score is smaller. c. The baby born in week 32 does since its z-score is larger. d. The baby born in week 41 does since its z-score is smaller.

Answer 1

The 32 week gestation's period baby weighs 0.31 standard deviations below the mean.

The 41 week gestation's period baby weighs 0.65 standard deviations below the mean.

The 41 week gestation's period baby weighs relatively less.

Explanation:

Normal model problems can be solved by the zscore formula.

On a normaly distributed set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a value X is given by:

`Z = (X - \mu)/(\sigma)`

The zscore represents how many standard deviations the value of X is above or below the mean
`\mu`.

Find the corresponding z-scores.

Babies born after a gestation period of 32 to 35 weeks have a mean weight of 2700 grams and a standard deviation of 800 grams. A 32-week gestation period baby weighs 2450.

Here, we have
`\mu = 2700, \sigma = 800, X = 2450`.

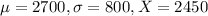So

`Z = (X - \mu)/(\sigma)`

`Z = (2450 - 2700)/(800)`

`Z = -0.31`

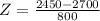
A negative z-score indicates that the value is below the mean.

So, the 32 week gestation's period baby weighs 0.31 standard deviations below the mean.

Babies born after a gestations period of 40 weeks have a mean weight of 2900 grams and a standard deviation of 385 grams. A 41 week gestation period baby weights 2650 grams.

Here, we have
`\mu = 2900, \sigma = 385, X = 2650`

`Z = (X - \mu)/(\sigma)`

`Z = (2650 - 2900)/(385)`

`Z = -0.65`

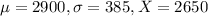
So, the 41 week gestation's period baby weighs 0.65 standard deviations below the mean.

Which baby weighs relatively less?

The 41 week gestation's period baby has a lesser z-score, so this means that he weighs relatively less.