Answer:
a) - 1.13
b) The speed of 25 mph is more unusual.
Explanation:
Given:
Speed limit = 35 mph
Mean of speeds, μ = 38.74 mph
standard deviation, σ = 3.31 mph
a) Now,
thus,
for x = 35 mph

here,
z is the deviation from the mean
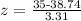
or
z = - 1.129 ≈ - 1.13
b) now,
for x = 48
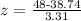
or
z = 2.79
and, for x = 25 mph

or
z = -4.15
on comparing the results we can see that 25 mph is more deviated from the mean, thus the speed of 25 mph is more unusual.