Question

(Geometry) The midpoint of CD is

E (–1, 0). One endpoint is C (5, 2).
What are the coordinates of the other endpoint?

Please explain this step by step, I am really struggling I want to learn how to do this for the future.

Answer 1

D(0,5)

Explanation:

for me I first had to mark the points on a graph then I connected the dots I know then point C I had to connect straight down to x (0) and it made a right angle. I hope that helps make sure to ask me more questions I'm free to help

Answer 2

D(-7,-2)

Explanation:

Formula for midpoint:

`Midpoint=((x_1+x_2)/(2),(y_1+y_2)/(2))`

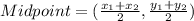
It is given that the midpoint of CD is E (–1, 0) and the coordinates of C are (5,2).

Let the coordinates of other endpoint are (a,b), then coordinates of E are

`E=((5+a)/(2),(2+b)/(2))`

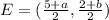
It is given that the coordinates of E are (–1, 0).

`(-1,0)=((5+a)/(2),(2+b)/(2))`

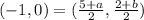
On comparing both sides we get

`(5+a)/(2)=-1`

`5+a=-2`

`a=-2-5`

`a=-7`

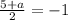
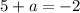
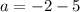
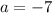
The value of a is -7.

`(2+b)/(2)=0`

`2+b=0`

`b=-2`

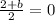
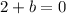
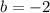
The value of b is -2.

Therefore the coordinates of the other endpoint are D(-7,-2).