Question

(From an actuarial exam) A company offers a health insurance plan, a life insurance plan, and an investment insurance plan. An employee can have 0, 1, or 2 plans, but cannot have both life insurance and investment plans. You are given the following information: • 450 employees have at least one plan. • 330 employees have only one plan. • 320 employees have the health insurance plan. • 45 employees have only the life insurance plan. • There are 20 more employees that have both health and life plans than those that have both health and investment plans. How many people have the investment plan

Answer 1

Explanation:

We can work with these values as a set value, and build a Venn Diagram from them.

I am going to say the set A are those that have the health insurance plan.

Set B are those that have the life insurance plan

Set C are those that have the investment plan.

We have that:

`A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)`

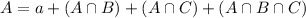
In which a is the number of employees that only have the health insurance plan,
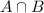`A \cap B` is the number of employees that have both the health and the life insurance plans,
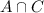`A \cap C` is the number of employees that have both the health insurance and the investment plans. and
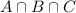`A \cap B \cap C` is the number of employees that have all three of those plans.

By the same logic, we have that:

`B = b + (A \cap B) + (B \cap C) + (A \cap B \cap C)`

`C = c + (B \cap C) + (A \cap C) + (A \cap B \cap C)`

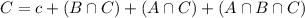
The problem states that:

An employee cannot have both life insurance and investment plans. So:

`B \cap C = 0, A \cap B \cap C = 0`

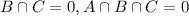
45 employees have only the life insurance plan. So:

`b = 45`

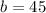
There are 20 more employees that have both health and life plans than those that have both health and investment plans

`A \cap B = A \cap C + 20`

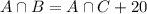
320 employees have the health insurance plan.

`A = 320`

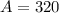
450 employees have at least one plan

`a + b + c + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 450`

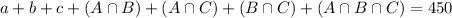
330 employees have only one plan

`a + b + c = 330`

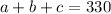
How many people have the investment plan?

We have to find the value of C.

Now we solve:

`a + b + c + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 450`

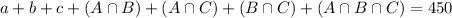
Applying what we have

-----------

`a + b + c + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 450`

`330 + A \cap C + 20 + A \cap C = 450`

`2(A\capC) = 100`

`A \cap C = 50`

`A \cap B = A \cap C + 20 = 50 + 20 = 70`

----------------

`A = 320`

`A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)`

`a + 70 + 50 = 320`

`a = 200`

------------------

`b = 45`

`a + b + c = 330`

`245 + c = 330`

`c = 85`

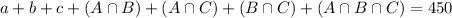
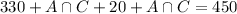
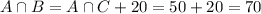
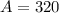
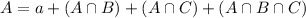
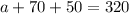
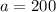
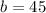
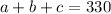
The number of people that have the investment plan is:

`C = 85 + 50 = 135`

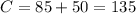
135 people have the investment plan