Question

A spherical shell of radius Ra carries a total charge qa uniformly distributed on its surface. A larger spherical shell of radius Rb is concentric with the first and carries a charge qb uniformly distributed on its surface. (a) Use Gauss’ law to find E~ in all regions (do not forget the inside of the smaller shell!). (b) If qa=6nC, what should qb be for the electric field to be zero for r > Rb? (c) Sketch the electric-field lines for the situation in part (b).

Answer 1

Step-by-step explanation:

Part a)

For a position of point inside the inner shell we can use Gauss law as

`\int E. dA = (q)/(\epsilon_0)`

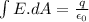
now here we know that enclosed charge in the inner shell is ZERO

so we have

`\int E. dA = 0`

`E = 0`

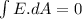
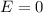
Now for the position between two shells

`r_a< r< r_b`

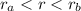
again by Gauss law

`\int E. dA = (q)/(\epsilon_0)`

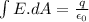
now here we know that enclosed charge between two shells is given as

`q = q_a`

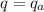
so we have

`\int E. dA = (q_a)/(\epsilon_0)`

`E = (q_a)/(4\pi \epsilon_0 r^2)`

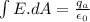
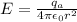
Now for position outside the shell we will have

`r > r_b`

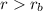
again by Gauss law

`\int E. dA = (q)/(\epsilon_0)`

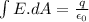
now here we know that enclosed charge given as

`q = q_a + q_b`

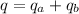
so we have

`\int E. dA = (q_a + q_b)/(\epsilon_0)`

`E = (q_a + q_b)/(4\pi \epsilon_0 r^2)`

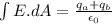
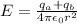
Part b)

If outside the shell net electric field is zero

then we can say

`q_a + q_b = 0`

`q_a = 6 nC`

`q_b = - 6nC`

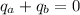
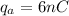
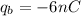
Part c)