Answer:
The source is at a distance of 4.56 m from the first point.
Solution:
As per the question:
Separation distance between the points, d = 11.0 m
Sound level at the first point, L = 66.40 dB
Sound level at the second point, L'= 55.74 dB
Now,
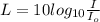
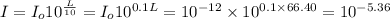
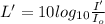
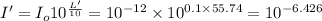
where
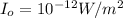
I = Intensity of sound
Now,
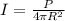
Similarly,
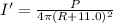
Now,
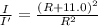
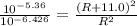
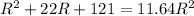
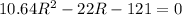
Solving the above quadratic eqn, we get:
R = 4.56 m