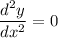Question

Find d 2 y over d x squared for the curve given by x = 2t + 5 and y equals 3 times t over 2 . (4 points) 3 over the quantity 4 times t plus 10 the quantity 4 times t plus 10 over 3 1 0

Answer 1

`(d^2y)/(dx^2)=0`

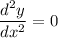
D is correct.

Explanation:

Given:
`x(t)=2t+5`

`y(t)=(3t)/(2)`

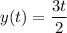
To find:
`(d^2y)/(dx^2)`

As we know,

`(dy)/(dx)=((dy)/(dt))/((dx)/(dt))`

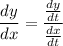
This is parametric equation. Differentiate both function separately and substitute into formula.

`x(t)=2t+5` and
`y(t)=(3t)/(2)`

`(dx)/(dt)=2,(y)/(dt)=(3)/(2)`

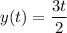
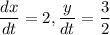
Substitute into derivative

`(dy)/(dx)=(3)/(2\cdot 2)=(3)/(4)`

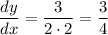
For double derivative differentiate w.r.t x

`(d^2y)/(dx^2)=0`

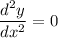
Hence, The value of
`(d^2y)/(dx^2)=0`