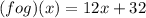Answer:
Part 1)
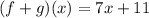
Part 2)

Part 3)
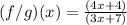
Part 4) In interval notation the domain is (-∞,-7/3) ∪ (-7/3,∞)
Part 5)
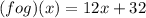
Explanation:
we have
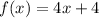
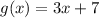
Part 1) Find (f+g)(x)
we know that
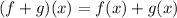
substitute the given functions
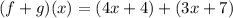
Combine like terms
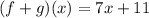
Part 2) Find (f-g)(x)
we know that
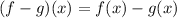
substitute the given functions
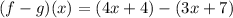
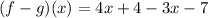
Combine like terms

Part 3) Find (f/g)(x)
we know that
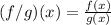
substitute the given functions
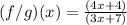
Part 4) What the domain for the answer in question 3
we have
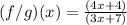
we know that
The denominator of the quotient cannot be equal to zero
so
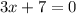
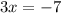
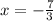
The domain is all real numbers except the number x=-7/3
In interval notation the domain is (-∞,-7/3) ∪ (-7/3,∞)
Part 5) Find (f o g) (x)
we know that
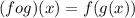
substitute
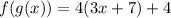

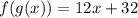
therefore