Question

The intensity I of light​ (measured in​ foot-candles) varies inversely with the square of the distance from the source. Suppose that the intensity of a light from the source at a distance of 2 meters is 0.065 ​foot-candle. Determine the intensity of a light from the source at a distance of 10 meters.

Answer 1

The intensity of a light from the source at a distance of 10 meters would be 0.0052 foot-candle.

Step-by-step explanation:

The intensity of light (measured in foot-candles) varies inversely with the square of the distance from the source. To determine the intensity of a light from the source at a distance of 10 meters, we can use the concept of the inverse square law for light. If the intensity at a distance of 2 meters is 0.065 foot-candle, we can calculate the new intensity using the equation:

I1/I2 = (d2^2)/(d1^2)

Plugging in the values, we have:

0.065/I2 = (10^2)/(2^2)

Simplifying the equation, we get:

I2 = 0.065 * (2^2)/(10^2) = 0.0052 foot-candle

Therefore, the intensity of a light from the source at a distance of 10 meters would be 0.0052 foot-candle

Answer 2

The intensity of a light from the source at a distance of 10 meters is 0.0026 foot-candle.

Step-by-step explanation:

Given that,

Distance from the source = 2 meter

Intensity = 0.065 foot -candle

New distance = 10 m

We know that,

The intensity I of light​ varies inversely with the square of the distance from the source.

We need to calculate the value of constant

Using formula of intensity

`I=(k)/(x^2)`

Put the value into the formula

`0.065=(k)/(6.56168^2)`

`k=0.065*(6.56168)^2`

`k=2.798`

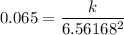
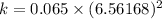
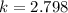
We need to calculate the intensity

Using formula of intensity again

`I=(k)/(x^2)`

Put the value into the formula

`I=(2.798)/(32.8084^2)`

`I=0.0026\ foot-candle`

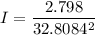
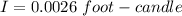
Hence, The intensity of a light from the source at a distance of 10 meters is 0.0026 foot-candle.