Question

Suppose car models A, B, and C are popular among drivers. Suppose 12% of the drivers own model A car, 30% own model B, 26% own model C, 3% own all three models, 5% own models A and B, 12% own models B and C, and 9% own models C and A. What proportion of the drivers do not have any of these three car models (round off to second decimal place)?

Answer 1

0.55

Explanation:

Let 100 be the number of all car owners.

• 12% of the drivers own model A car, then 12 drivers own car A;
• 30% own model B, then 30 drivers own car B;
• 26% own model C, then 26 drivers own car C;
• 3% own all three models, then 3 drivers own all 3 cars;
• 5% own models A and B, then 5 drivers own cars A and B;
• 12% own models B and C, then 12 own cars B and C;
• 9% own models C and A, then 9 drivers own cars A and C.

Now,

• 3 drivers own all three cars;
• 5 - 3 = 2 drivers own only cars A and B;
• 12 - 3 = 9 drivers own only cars B and C;
• 9 - 3 = 6 drivers own only cars A and C;
• 12 - 3 - 2 - 6 = 1 driver owns only car A;
• 30 - 3 - 2 - 9 = 16 drivers own only car B;
• 26 - 3 - 9 - 6 = 8 drivers own only car C.

In total, there are

3 + 2 + 9 + 6 + 1 + 16 + 8 = 45 dirvers own cars A, B or C.

Thus,
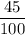`(45)/(100)` of drivers own cars A, B or C and
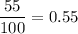`(55)/(100)=0.55` do not own cars A, B, C.