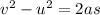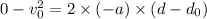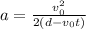Question

To practice Problem-Solving Strategy 2.1 for constant acceleration problems. A car is traveling at a constant velocity of magnitude v0 when the driver notices a garbage can on the road in front of him. At that moment, the distance between the garbage can and the front of the car is d. A time t after noticing the garbage can, the driver applies the brakes and slows down at a constant rate before coming to a halt just before the garbage can. What is the magnitude of the car's acceleration after the brakes are applied?

Answer 1

Answer:
`a=(v_0^2)/(2(d-v_0t))`

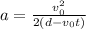
Step-by-step explanation:

Given

Velocity of car is
`v_0`

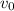
distance between car and can is d

reaction time is t

Distance traveled in reaction time

let say
`d_0`

`d_0=v_0t`

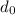
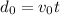
Remaining distance
`=d-d_0`

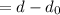
Now final velocity of car will be zero after applying brakes

Using equation of motion

`v^2-u^2=2as`

`0-v_0^2=2* (-a)* (d-d_0)`

`a=(v_0^2)/(2(d-v_0t))`