Question

1 From t = 0 to t = 5.00 min, a man stands still, and from t = 5.00 min to t = 10.0 min, he walks briskly in a straight line at a constant speed of 2.20 m/s. What are (a) his average velocity vavg and (b) his average acceleration aavg in the time interval 2.00 min to 8.00 min? What are (c) vavg and (d) aavg in the time interval 3.00 min to 9.00 min? (e) Sketch x versus t and v versus t, and indicate how the answers to (a) through (d) can be obtained from the graphs.

Answer 1

Step-by-step explanation:

Part a)

For time interval of 2.00 min to 8.00 min

we know that

`v_(avg) = (displacement)/(time)`

from t = 5 min to t = 8 min distance moved by him

`d = 2.20* 3* 60`

`d = 396 m`

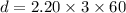
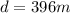
now we have

`v_(avg) = (396)/((8 - 2)* 60)`

`v_(avg) = 1.1 m/s`

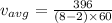
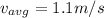
Part b)

for average acceleration we know that

`a = (\Delta v)/(\Delta t)`

`a = (2.20 - 0)/((8.00 - 2.00)* 60)`

`a = 0.0611m/s^2`

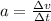
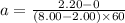
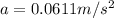
Part c)

now we need to find average velocity from t = 3.00 m to 9.00 m

so we will have

`d = 2.20* 4* 60`

`d = 528 m`

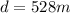
now we have

`v_(avg) = (528)/((9 - 3)* 60)`

`v_(avg) = 1.47 m/s`

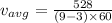
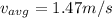
Part d)

for average acceleration we know that

`a = (\Delta v)/(\Delta t)`

`a = (2.20 - 0)/((9.00 - 3.00)* 60)`

`a = 0.0611m/s^2`

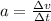
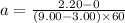
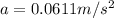
Part e)

We can find the average velocity by finding the slope of the chord on x - t graph for given interval of time

and to find the average acceleration we can find the slope of velocity time graph to given interval