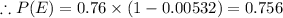Question

Trucks that travel on highways have to stop at various locations to be weighed and inspected for safe brakes and light systems. Of these​ trucks, 76​% are on interstate commerce while 24​% are intrastate. Of the intrastate​ trucks, 3.4​% are flagged for safety defects compared to 0.7​% of those that are on interstate business. Complete parts a through c below. a. Calculate the probability that a randomly chosen truck is an interstate truck and is not flagged for a safety violation. The probability is nothing. ​(Round to three decimal places as​ needed.)

Answer 1

The reuired probability is 0.756

Explanation:

Let the number of trucks be 'N'

1) Trucks on interstate highway N'= 76% of N =0.76N

2) Truck on intra-state highway N''= 24% of N = 0.24N

i) Number of trucks flagged on intrastate highway = 3.4% of N'' =
`(3.4)/(100)* 0.24N=0.00816N`

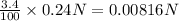
ii) Number of trucks flagged on interstate highway = 0.7% of N' =
`(0.7)/(100)* 0.76N=0.00532N`

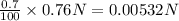
Part a)

The probability that the truck is an interstate truck and is not flagged for safety is
`P(E)=P_(1)* (1-P_(2))`

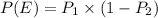
where

`P_(1)` is the probability that the truck chosen is on interstate

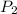`P_(2)` is the probability that the truck chosen on interstate is flagged

`\therefore P(E)=0.76* (1-0.00532)=0.756`