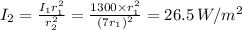Answer:
various parts have been answered
Step-by-step explanation:
Inverse square for light is
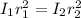
initial distance from sun to earth is
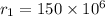
and intensity or apparent brightness of sun is
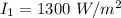
a)
If distance from sun to earth is
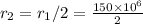
then apparent brightness is
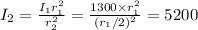
b)
If distance from sun to earth is
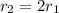
then apparent brightness is
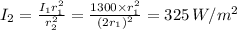
c)
If distance from sun to earth is

then apparent brightness is